Содержание
зачем она нужна и на что влияет?
Редакция сайта
Теги:
Интересные факты
природа
Все мы знаем, что симметрия — это залог красоты. Вы ведь наверняка слышали утверждение о том, что «правильные» лица подсознательно кажутся нам красивыми.
Item 1 of 2
1 / 2
Автор популярного YouTube-блога «ТОПЛЕС» решил разобраться в том, как симметрия и асимметрия влияют на все, что происходит на нашей планете. Подготовка ролика потребовала двухмесячной работы, так что настоятельно рекомендуем ознакомиться с уникальным контентом, созданным командой блога.
А знали ли вы, что улитки с разным типом раковины (то есть закрученными в разные стороны) не могут стать парой? Это потому, что половые органы у них расположены зеркально.
Item 1 of 2
1 / 2
Когда-то была найдена уникальная улитка, которую назвали Джереми. У этого милашки как раз была раковина, закрученная «не в ту сторону» — влево. BBC начали флешмоб под названием «улиточная любовь» с целью найти Джереми партнершу. Любовь с такой же «неправильной» раковиной была найдена, и у пары даже появились дети. Интересно, что у малышей раковины оказались вполне обычными, закрученными вправо.
Item 1 of 5
1 / 5
Когда же мир стал делиться? И почему это так важно?
Идеальная симметрия (сферическая) наблюдается у одноклеточных. Но шариком можно оставаться, только будучи очень маленьким, существа потяжелее переходят на другой уровень симметрии — радиальный. Вспомните морских звезд, гидр и медуз: первых можно повернуть аж 5 раз, чтобы получить то же самое.
Вспомните морских звезд, гидр и медуз: первых можно повернуть аж 5 раз, чтобы получить то же самое.
Но когда нужно эволюционировать, охотиться и быстро передвигаться, симметрии становится все меньше. Например, передняя часть тела начинает отличаться от задней. Билатеральная симметрия отлично подходит для движения вперед. Это относится и к людям: левая и правая части нашего тела симметричны.
А вскрыл этот код небезызвестный Алан Тьюринг. Увы, механизм иногда дает сбой, и иногда симметрия появляется там, где ее не должно быть. А как же растения, спросите вы. Кажется, в мире флоры царит хаос, но это не совсем так — это просто фрактальная симметрия. Эта система позволяет доставлять ресурсы к самым отдаленным участкам.
А знали ли вы, что у одного из 20 000 человек случается инверсия? То есть сердце находится не слева, а справа. А вместе с ним смещены и печень, и другие органы, например, аппендикс. И это случается не так уж редко — инверсия есть у Энрике Иглесиаса, например.
Так почему же не весь мир симметричен? И на что влияет асимметрия? Оказывается, она пришла из космоса. Осознавали ли вы, что мы результат борьбы материи и антиматерии (по сути — правого и левого)? Как это произошло? «Объяснение на пальцах» ждет в ролике от «ТОПЛЕС»:
youtube
Нажми и смотри
Симметрия вокруг нас | Образовательная социальная сеть
Слайд 1
Симметрия вокруг нас Выполнила : ученица 5 Л класса МБОУ “ СОШ №39» Дубова Ольга Руководитель: Дубова П. С.
Слайд 2
Цель: Ознакомиться с симметрией в математике, природе, технике, быту, искусстве, русском языке Узнать для чего нужна симметрия
Слайд 3
Введение С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековым замкам, современным зданиям она придает гармоничность и законченность. Симметрия буквально пронизывает весь окружающий нас мир
Слайд 4
Определение В древности слово «симметрия» употреблялось как «гармония» и «красота». По-гречески оно означает «соразмерность, пропорциональность, одинаковость в расположении частей».
По-гречески оно означает «соразмерность, пропорциональность, одинаковость в расположении частей».
Слайд 5
Содержание Симметрия в математике Симметрия в природе Симметрия в технике Симметрия в быту Симметрия в искусстве Симметрия в русском языке
Слайд 6
Симметрия в математике 1 вид симметрии Центральная симметрия Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1. Точка О считается симметричной самой себе.
Слайд 7
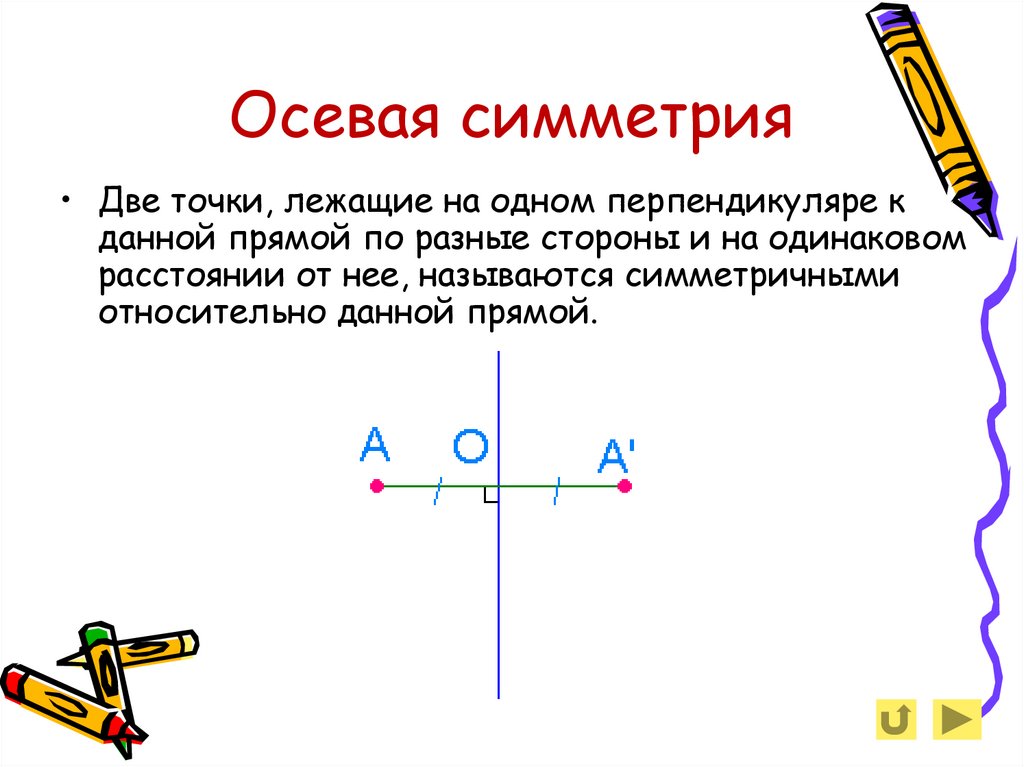
Осевая симметрия 2 вид Две точки А и А1, лежащие на одном перпендикуляре к данной прямой по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно данной прямой.
Слайд 8
Симметричные фигуры На рисунке снежинка имеет 1 центр симметрии и 6 осей симметрии
Слайд 9
Фигуры, обладающие одной осью симметрии Угол Равнобедренный треугольник Равнобедренная трапеция
Слайд 10
Фигуры, обладающие двумя осями симметрии Прямоугольник Ромб
Слайд 11
Фигуры, имеющие более двух осей симметрии Равносторонний треугольник Квадрат Круг
Слайд 12
Фигуры, не обладающие осевой симметрией Произвольный треугольник Параллелограмм Неправильный многоугольник
Слайд 13
Симметрия в природе По мнению, ученого-энциклопедиста академика В. И. Вернадского, симметрия окружает нас повсюду. В 19-м веке исследования в этой области привели к заключению, что симметрия природных форм зависит от влияния сил земного тяготения, которое в каждой точке имеет симметрию конуса.
И. Вернадского, симметрия окружает нас повсюду. В 19-м веке исследования в этой области привели к заключению, что симметрия природных форм зависит от влияния сил земного тяготения, которое в каждой точке имеет симметрию конуса.
Слайд 14
Симметрия в физике и не живой природе
Слайд 16
Симметрия в атмосфере 27 января 2013 года в г. Алатырь при восходе солнца, около реки Суры наблюдалось интересное явление, солнечные световые столбы. Это явление природы возникает при сильном морозе, когда солнечный свет отражается в кристализованных осадках в атмосфере
Слайд 17
Каждая снежинка – это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией Все твердые тела состоят из кристаллов
Слайд 18
Симметрия в мире животных В природе наиболее распространены два вида симметрии — зеркальная и лучевая симметрии. Зеркальной симметрией обладает бабочка, листок или жук и часто такой вид симметрии называется «симметрией листка» или «билатеральной симметрией». Можно сказать, что каждое животное (а также насекомое, рыба, птица) состоит из двух: правой и левой половин.
Можно сказать, что каждое животное (а также насекомое, рыба, птица) состоит из двух: правой и левой половин.
Слайд 20
Симметрия у растений К формам с лучевой симметрией относятся гриб, ромашка, сосновое дерево и часто такой вид симметрии называется » ромашково-грибной » симметрией
Слайд 21
Симметрия у человека Человеческое тело также обладает билатеральной симметрией. Но если разделить человеческое тело пополам, то можно заметить, что не каждая его часть равна. У кого-то правая нога длиннее левой, или рука, пальцы и т.д. Человек с идеально симметричным телом считается красивым, здоровым. А не симметричность служит, по -мнению врачей, признаком какого-нибудь заболевания. Например, по симметричности лица новорожденных судят о здоровье его мозга и нервной системы. Мозг человека состоит из двух частей-полушарий, плотно прилегающих друг к другу. Каждое полушарие почти точное зеркальное отображение другого. В Японии с детства развивают оба полушария. Так японцы могут писать одинаково левой и правой рукой. И в случае поражения какого-то полушария, его работу выполняет другое полушарие, и функции человека не нарушаются.
И в случае поражения какого-то полушария, его работу выполняет другое полушарие, и функции человека не нарушаются.
Слайд 22
Винтовая Симметрия Этот вид симметрии часто встречается в растениях, кристаллах, ракушках и т.п.
Слайд 23
Симметрия в технике Симметрия в технике наблюдается очень часто. Я думаю люди это делают, потому что такой техникой удобнее пользоваться.
Слайд 24
Симметрия в быту Орнамент и бордюры
Слайд 25
Симметрия в архитектуре
Слайд 26
Симметрия в поэзии и музыке «Душа музыки – ритм – состоит в правильном периодическом повторении частей музыкального произведения, — писал в 1908 году известный русский физик Г.В. Вульф. – Правильное же повторение одинаковых частей в целом и составляет сущность симметрии. В стихотворениях подразумевается симметрия чередования рифм, ударных слогов. Композитор в своей симфонии может по нескольку раз возвращаться к одной и той же теме, постепенно разрабатывая ее. Все ярко, все бело круг ом . На стеклах легкие уз оры , Сорок веселых на дво ре , Деревья в зимнем сереб ре, И мягко устланные г оры Зимы блистательным ковр ом Пушкин А.С. «Евгений Онегин»
На стеклах легкие уз оры , Сорок веселых на дво ре , Деревья в зимнем сереб ре, И мягко устланные г оры Зимы блистательным ковр ом Пушкин А.С. «Евгений Онегин»
Слайд 27
Симметрия в русском языке Буквы А, М, Т, Ш, П имеют вертикальную ось симметрии В, З, К, С, Э, Е – горизонтальную. А буквы Ж, Н, О, Ф, Х имеют по две оси симметрии. Симметрию можно увидеть и в словах: казак, шалаш. Есть и целые фразы с таким свойством (если не учитывать пробелы между словами). Такие фразы называются палиндромами. “Искать такси” “Аргентина манит негра” “Ценит негра аргентинец” “ А роза упала на лапу Азора ” Палиндром В.Набокова: Я ел мясо лося, млея… Рвал Эол алоэ, лавр.
Слайд 28
Заключение Симметрию можно обнаружить почти везде. Для человека –это уравновешенность и гармония. По словам немецкого математика Германа Вейля: « Посредством симметрии человек всегда пытался постичь и создать порядок, красоту и совершенство». О симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, в малой мошке, Ты в елочке, что у лесной дорожки. С тобою в дружбе и тюльпан, и роза, И снежный рой – творение мороза!
С тобою в дружбе и тюльпан, и роза, И снежный рой – творение мороза!
Слайд 29
Спасибо за внимание
Симметрия – определение, типы, примеры
В математике симметрия означает, что одна фигура идентична другой, когда ее перемещают, поворачивают или переворачивают. Если объект не имеет симметрии, мы говорим, что объект асимметричен. Понятие симметрии обычно встречается в геометрии.
| 1. | Что такое симметрия в математике? |
| 2. | Линия симметрии |
| 3. | Типы симметрии |
| 4. | Что такое точечная симметрия? |
| 5. | Часто задаваемые вопросы о Symmetry |
Что такое симметрия в математике?
Форма или объект имеет симметрию, если его можно разделить на две одинаковые части. В симметричной форме одна половина является зеркальным отражением другой половины. Воображаемая ось или линия, по которой можно сложить фигуру, чтобы получить симметричные половины, называется линией симметрии.
Воображаемая ось или линия, по которой можно сложить фигуру, чтобы получить симметричные половины, называется линией симметрии.
Определение симметрии
Фигура называется симметричной, если ее можно разделить на две более идентичные части, расположенные упорядоченным образом. Например, когда вам говорят вырезать «сердце» из листа бумаги, вы просто сгибаете бумагу, рисуете половину сердца на сгибе и вырезаете его, чтобы обнаружить, что вторая половина точно соответствует первой. половина. Вырезанное сердце является примером симметрии. Точно так же правильный пятиугольник, разделенный, как показано на изображении ниже, имеет одну часть, симметричную другой.
Определение симметрии в математике гласит, что «симметрия — это зеркальное отображение», т. е. когда изображение выглядит идентично исходному изображению после поворота или переворачивания формы, тогда это называется симметрией. Симметрия существует в шаблонах. Это сбалансированное и пропорциональное сходство, обнаруживаемое в двух половинках объекта, что означает, что одна половина является зеркальным отражением другой половины. Симметричные объекты встречаются повсюду вокруг нас в повседневной жизни, в искусстве и архитектуре.
Симметричные объекты встречаются повсюду вокруг нас в повседневной жизни, в искусстве и архитектуре.
Линия симметрии
Линия симметрии — это линия, которая делит объект на две одинаковые части. Здесь у нас есть звезда, и мы можем сложить ее на две равные половины. Когда фигуру складывают пополам по линии симметрии, обе половинки точно совпадают друг с другом. Эта линия симметрии называется осью симметрии.
Линия симметрии может быть классифицирована в зависимости от ее ориентации как:
- Вертикальная линия симметрии
- Горизонтальная линия симметрии
- Диагональная линия симметрии
Вертикальная линия симметрии
Вертикальная линия симметрии — это линия, идущая вертикально вниз и делящая изображение на две одинаковые половины. Например, следующую фигуру можно разделить на две одинаковые половины стоящей прямой линией. В этом случае линия симметрии вертикальна.
Горизонтальная линия симметрии
Горизонтальная линия симметрии делит фигуру на одинаковые половины при горизонтальном разрезе, т. е. при разрезе справа налево или наоборот. Например, следующую фигуру можно разделить на две равные половины при горизонтальном разрезе. В этом случае линия симметрии горизонтальна.
е. при разрезе справа налево или наоборот. Например, следующую фигуру можно разделить на две равные половины при горизонтальном разрезе. В этом случае линия симметрии горизонтальна.
Диагональная линия симметрии
Диагональная линия симметрии делит фигуру на одинаковые половины при разделении диагональными углами. Например, мы можем разделить следующий квадрат по углам, чтобы сформировать две одинаковые половины. В этом случае линия симметрии является диагональной.
Линия симметрии — это ось, вдоль которой объект при разрезании будет иметь одинаковые половины. Эти объекты могут иметь одну, две или несколько линий симметрии.
- Одна линия симметрии
- Две линии симметрии
- Бесконечные линии симметрии
Одна линия симметрии
Фигуры с одной линией симметрии симметричны только относительно одной оси. Он может быть горизонтальным, вертикальным или диагональным. Например, буква «А» имеет одну линию симметрии, то есть вертикальную линию симметрии вдоль ее центра.
Две линии симметрии
Фигуры с двумя линиями симметрии симметричны только относительно двух линий. Линии могут быть вертикальными, горизонтальными или диагональными. Например, прямоугольник имеет две оси симметрии, вертикальную и горизонтальную.
Бесконечные линии симметрии
Фигуры с бесконечными линиями симметрии симметричны только относительно двух линий. Линии могут быть вертикальными, горизонтальными или диагональными. Например, прямоугольник имеет две оси симметрии, вертикальную и горизонтальную.
В следующей таблице показаны примеры различных форм с количеством осей симметрии, которые они имеют.
| Число осей симметрии | Примеры рисунков |
|---|---|
| Нет линии симметрии | Разносторонний треугольник |
| Ровно одна линия симметрии | Равнобедренный треугольник |
| Ровно две оси симметрии | Прямоугольник |
| Ровно три линии симметрии | Равносторонний треугольник |
Типы симметрии
Симметрию можно увидеть, когда вы переворачиваете, поворачиваете или перемещаете объект. Существует четыре типа симметрии, которые можно наблюдать в различных случаях.
Существует четыре типа симметрии, которые можно наблюдать в различных случаях.
- Трансляционная симметрия
- Вращательная симметрия
- Рефлексивная симметрия
- Симметрия скольжения
Трансляционная симметрия
Если объект перемещается из одного положения в другое с одинаковой ориентацией при движении вперед и назад, это называется трансляционной симметрией. Другими словами, трансляционная симметрия определяется как скольжение объекта вокруг оси. Например, на следующем рисунке, где фигура перемещается вперед и назад в одной и той же ориентации, сохраняя фиксированную ось, изображена поступательная симметрия.
Вращательная симметрия
Когда объект вращается в определенном направлении вокруг точки, это называется вращательной симметрией, также известной как радиальная симметрия. Вращательная симметрия существует, когда форма повернута, и форма идентична началу координат. Угол вращательной симметрии — это наименьший угол, на который можно повернуть фигуру, чтобы она совпала с самой собой, а порядок симметрии — это то, как объект совпадает с самим собой, когда он вращается.
В геометрии есть много фигур, изображающих вращательную симметрию. Например, такие фигуры, как круг, квадрат, прямоугольник изображают вращательную симметрию. На следующем изображении показано, как структура морской звезды следует вращательной симметрии. Если вы повернете или повернете морскую звезду вокруг точки P, она все равно будет выглядеть одинаково со всех сторон. Знаменитое колесо обозрения, Лондонский глаз, является примером вращательной симметрии. В реальной жизни можно найти много объектов, обладающих вращательной симметрией, таких как колеса, ветряные мельницы, дорожные знаки, потолочные вентиляторы и так далее.
Рефлексивная симметрия
Отражающая симметрия, также называемая зеркальной симметрией, представляет собой тип симметрии, при котором одна половина объекта отражает другую половину объекта. Например, в целом человеческие лица одинаковы слева и справа.
Симметрия скольжения
Симметрия скольжения представляет собой комбинацию трансляционных и отражательных преобразований. Скользящее отражение коммутативно по своей природе, и изменение порядка комбинации не меняет выход скользящего отражения.
Скользящее отражение коммутативно по своей природе, и изменение порядка комбинации не меняет выход скользящего отражения.
Забавные факты о симметрии
- Внутри калейдоскопа есть зеркала, которые создают изображения с несколькими линиями симметрии. Угол между зеркалами определяет количество линий симметрии.
- Возможно, в повседневной жизни мы наблюдали несколько симметричных объектов, таких как ранголи или коламы. Поразительный аспект симметрии можно наблюдать в дизайне ранголи. Эти узоры известны в Индии своими уникальными и симметричными узорами. Они изображают красочную науку о симметрии.
Что такое точечная симметрия?
Объект имеет точечную симметрию, если каждая часть объекта имеет соответствующую часть. Многие буквы английского алфавита имеют точечную симметрию. Точка O является центральной точкой, а соответствующие части находятся в противоположных направлениях.
Если объект выглядит одинаково, когда его переворачивают вверх ногами, говорят, что он обладает точечной симметрией. Форма и соответствующие части должны быть в противоположных направлениях.
Форма и соответствующие части должны быть в противоположных направлениях.
Важные примечания
Ниже приведены некоторые важные моменты, связанные с понятием симметрии:
- Все правильные многоугольники имеют симметричную форму. Количество линий симметрии равно количеству его сторон.
- Объект и его изображение симметричны относительно его зеркальной линии.
- Если фигура имеет вращательную симметрию 180º, то она имеет точечную симметрию.
☛Похожие темы
Ниже перечислены некоторые темы, связанные с симметрией.
- Квадрат
- Является ли квадрат прямоугольником
- Диагональ прямоугольника Формула
Часто задаваемые вопросы о Symmetry
Что такое симметрия в математике?
Симметрия определяется как пропорциональное и уравновешенное подобие, которое обнаруживается в двух половинах объекта, то есть одна половина является зеркальным отражением другой половины. Например, различные формы, такие как квадрат, прямоугольник, круг, симметричны относительно соответствующих им линий симметрии.
Например, различные формы, такие как квадрат, прямоугольник, круг, симметричны относительно соответствующих им линий симметрии.
Что такое симметричная форма?
Двухмерную фигуру можно назвать симметричной, если через нее можно провести линию, и каждая сторона является отражением другой. Например, квадрат имеет симметричную форму.
Какие существуют 4 типа симметрии?
Симметрию можно разделить на четыре типа:
- Трансляционная симметрия: если объект перемещается или перемещается из одного положения в другое, одинаковая ориентация при прямом и обратном движении называется трансляционной симметрией.
- Вращательная симметрия: Когда объект вращается в определенном направлении вокруг точки, это называется вращательной симметрией.
- Рефлексивная симметрия. Рефлексивная симметрия, также называемая зеркальной симметрией, представляет собой тип симметрии, при котором одна половина объекта отражает другую половину объекта.
- Симметрия скольжения: Симметрия скольжения представляет собой комбинацию трансляционных и отражательных преобразований.

Что означает симметрия? Объясните на примере.
Когда объект остается точно таким же, когда вы его поворачиваете или переворачиваете, этот объект обладает симметрией. Симметричные объекты имеют одинаковый размер и форму. В природе есть множество объектов, обладающих симметрией. Например, лепестки цветка, бабочки и т. д.
Что такое симметричный узор?
Все узоры, имеющие симметрию, называются симметричными узорами. Листья растений имеют различные узоры и формы. Большинство этих листьев изображают симметричные узоры, если принять среднюю жилку за линию вертикальной симметрии.
Что вы понимаете под линией симметрии?
Линия симметрии — это линия, которая делит объект на две одинаковые части. Например, диагональ квадрата делит его на две равные половины, это называется линией симметрии квадрата.
Может ли линия симметрии быть параллельной?
Нет, линия симметрии не может быть параллельной. Все линии симметрии, проведенные для любой фигуры, всегда будут совпадать друг с другом.
Что такое симметрия? — Факты определения и примеры
Симметрия
В математике, особенно в геометрии и ее приложениях, говорят, что объект обладает симметрией, если его можно разделить на две одинаковые половины. Например, посмотрите на данное изображение цветка:
Если бы мы провели воображаемую линию посередине цветка, мы могли бы разделить его на две равные части следующим образом:
Обратите внимание, что эти две части идентичны и зеркальны. изображения друг друга.
Объект, который не является симметричным, называется асимметричным. Это означает, что асимметричный объект нельзя разделить на одинаковые половины.
Примером асимметрии может быть данное изображение.
Рекомендуемые рабочие листы:
Линия симметрии
Давайте еще раз посмотрим на этот цветок, пунктирная линия, по которой мы разделили его на две одинаковые половины, называется линией симметрии или осью симметрии. Его также можно определить как линию, по которой мы можем сложить объект так, чтобы его левая и правая половины полностью перекрывали друг друга.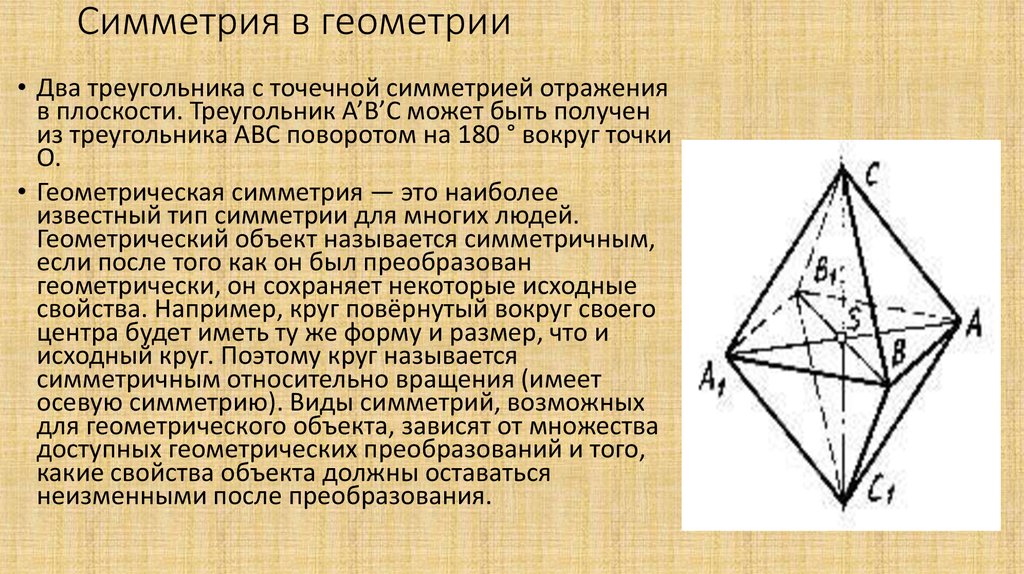
В математике есть три типа линий симметрии.
- Вертикальная линия симметрии
- Горизонтальная линия симметрии
- Диагональная линия симметрии
Давайте посмотрим на каждую из этих строк.
Вертикальная линия симметрии
Вертикальная линия, которая делит объект на две одинаковые половины, называется вертикальной линией симметрии. Это означает, что вертикальная линия идет сверху вниз (или наоборот) в объекте и делит его на зеркальные половины. Например, звезда ниже показывает вертикальную линию симметрии.
Горизонтальная линия симметрии
Когда горизонтальная линия делит объект на две одинаковые половины, она называется горизонтальной линией симметрии. Это означает, что горизонтальная линия симметрии проходит слева направо (или наоборот) в объекте. Например, на изображении ниже показана горизонтальная линия симметрии.
Диагональная линия симметрии
Когда диагональная/наклонная линия делит объект на две одинаковые половины, она называется диагональной линией симметрии.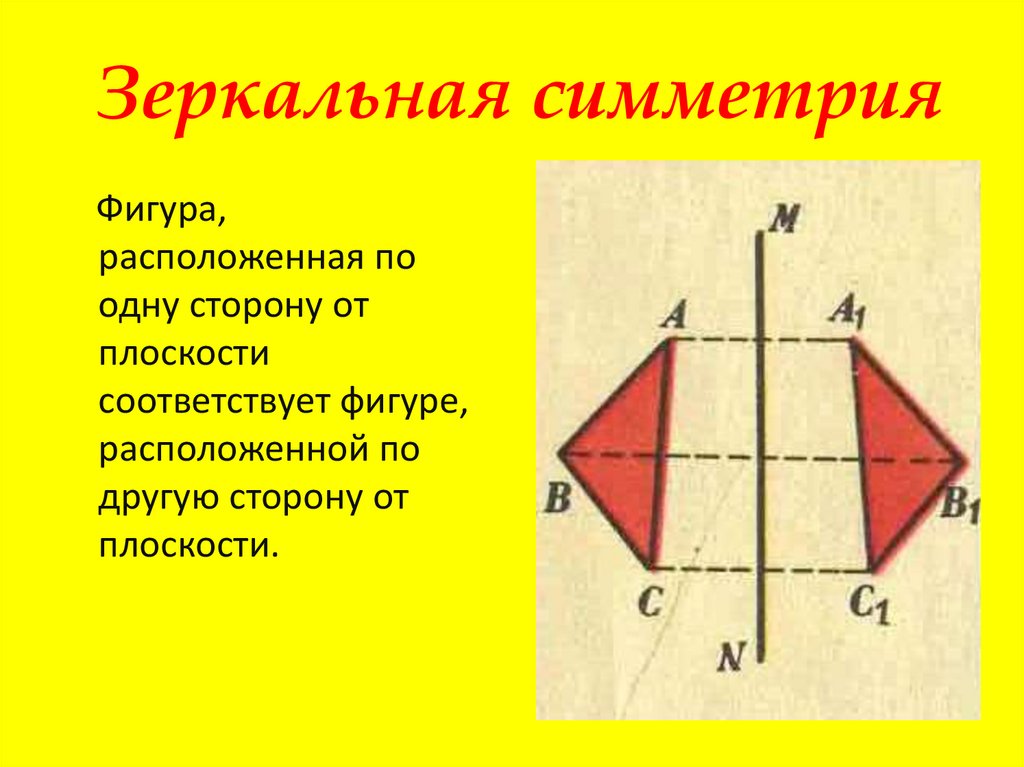 Например, квадрат ниже показывает диагональную линию симметрии.
Например, квадрат ниже показывает диагональную линию симметрии.
На самом деле квадрат обладает всеми тремя осями симметрии.
Таким образом, мы можем сказать, что объект может иметь несколько линий симметрии. Некоторыми другими примерами фигур, которые имеют несколько линий симметрии, являются круги и прямоугольники.
Примером фигуры, не имеющей линии симметрии, является разносторонний треугольник. Поскольку все стороны разностороннего треугольника различны, его нельзя разделить на две одинаковые зеркальные половины.
Симметрия в реальной жизни
Симметрии научила человека сама природа. Многие цветы и большинство животных симметричны по своей природе. Вдохновленные этим, люди научились строить свою архитектуру с симметричными аспектами, что делало здания сбалансированными и пропорциональными в их основании, как пирамиды Египта! Мы можем наблюдать симметрию вокруг себя во многих формах:
- Деревья, отражающиеся в кристально чистой воде, и высокие горы, отражающиеся в озере.

- Перья павлина и крылья бабочек и стрекоз имеют одинаковые левую и правую стороны.
- Ульи медоносных пчел имеют шестиугольную форму, которая по своей природе является симметричной.
- Зимние снежинки имеют все три оси симметрии.
Решенные примеры
Пример 1: Сколько осей симметрии имеет данная фигура?
Ответ: Только одна линия симметрии.
Пример 2. Можете ли вы найти примеры букв алфавита, которые имеют горизонтальную линию симметрии?
Ответ: Многие буквы, такие как O, D, H, имеют горизонтальные линии симметрии.
Пример 3: Является ли данная форма симметричной или асимметричной?
Ответ: Данная фигура симметрична относительно вертикальной линии симметрии.
Практические задачи
1
Сколько осей симметрии имеет прямоугольник?
2
3
1
4
Правильный ответ: 2
Прямоугольник имеет только две оси симметрии.
2
Какие из следующих букв алфавита имеют горизонтальную и вертикальную линии симметрии?
Y
X
P
M
Правильный ответ: X
Буква X имеет как вертикальные, так и горизонтальные линии симметрии.
3
Какую линию симметрии имеет следующая фигура?
Горизонт
Диагональ
Вертикаль
Линия симметрии отсутствует
Правильный ответ: Вертикальная
Данная фигура имеет только вертикальную линию симметрии
4
Какое из следующих чисел имеет две оси симметрии?
7
5
3
8
Правильный ответ: 8
Число 8 имеет две оси симметрии.
Часто задаваемые вопросы
Что такое симметрия в математике?
Симметрия в математике — это свойство объекта делиться на две одинаковые зеркальные половины.